Searching Algorithms是AI課堂中總會聽過的,而Searching Algorithms 分了好幾個的Search,以下會作淺談。
首先Searching Algorithms 分了Uniformed Search 和 Informed Search,當中最大的分別就是Uniformed Search 是不會考慮到將來的結果,即是沒有考慮過將來的Cost,而Informed Search是會考慮到將來的因素,包括將來的Cost。
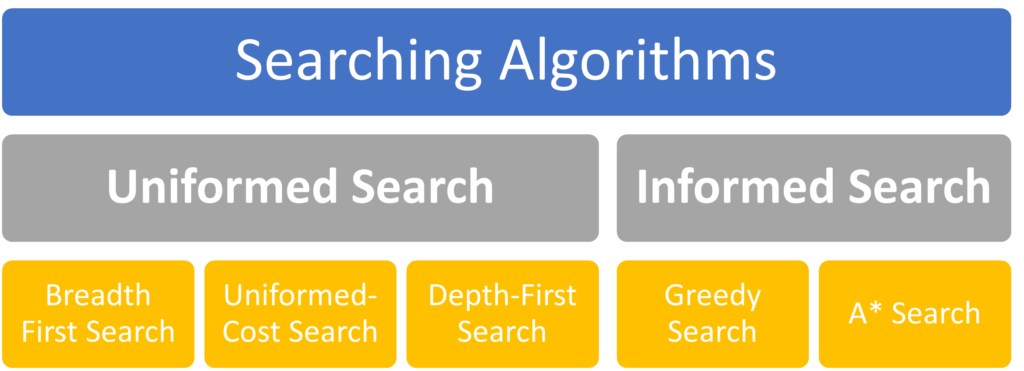
先來說說Uniformed Search – 這個Search就是只會用當中可供用的資料作處理,有3種Search: Breadth First Search,Uniformed-Cost Search,Depth-First Search。
先來說說第一個Breadth First Search,最大的特點就是由最淺(Shallowest)的層次(Layers)到最深的層次推進 ,再由先入先出的方式決定(First-in-First-out)。從完成度(Completeness)及最佳性(Optimal)來評論,Breadth First Search 是不能完全完成整個Searching Process,如果分支(Branching)是無限(infinite),相反,如果分支(Branching)是有限(finite)的,就可以完成搜索。 Breadth First Search 未能最佳化。
其次第二個是Uniformed-Cost Search,最大的特點就如其名一樣,重點是在Cost,Uniformed-Cost Search是要選擇最細的Cost,而Cost是最細的累積成本(cumulative cost),denote寫法是g(n),所以我們可以理解為選擇最低的g(n),如果步程的成本(Step Cost)是均等的,其實是和Breadth First Search一樣的。從完成度(Completeness)及最佳性(Optimal)來評論,Uniformed-Cost Search是十分理想的,可以完成Searching,因為Step Cost是不過少於0,少於0 Algorithms是未能進行的。最佳化來說是可以達到的,因為先考慮了最佳化的路程(Path)。
最後一個亦是第三個就是Depth First Search,最大的特點又是和名稱一樣,就是深度(Deepest),從越深度越向深探索,另外一個特點就是後入先出(Last-in-First-out)。從完成度(Completeness)及最佳性(Optimal)來評論,Depth First Search是未能完成整個Search過程,因為是有機會深度的分支(Depth-state)是無限的(infinite),而Optimal亦不算是,因為是由先後次序去決定。
接著來說說是Informed Search – 這個是有考慮到將來的成本(Cost),Best First Search 的目的就是為了最理想化地開發node,分為Greedy Search 和A* Search。Informed Search 可以說是heruistic,denote是h(n),即是經n到達最近目標(Goal)的估計成本(Estimated cost to closet goal through n node)。最理想的情況是h(n)是大過或等於實際的成本h*(n),所以就是最好不要超越實際的成本。
Greedy Search 是可以理解為f(n) = h(n),f(n)是由根點(Root)到目標的預計總成本(Estimated total cost from root node to goal through n node),Greedy Search 就是總預計的成本等於到達目標的成本。從完成度(Completeness)及最佳性(Optimal)來評論,Greedy Search 是未能完成的,無論是在有限(infinite)的Tree Search 或是在Graph Search當中,Graph Search 是在有限的State中可以完成,而在無限的State中未能完成,亦未能達到最佳化,需要依靠heruistic。
A* Search即是取得了Uniformed-Cost Search 和Greedy Search 的優點,考慮了過往的成本和將來的成本所產生的,可以理解為f(n) = g(n) + h(n),g(n)在Uniformed-Cost Search已經出現了,g(n)是path cost from root to n node。從完成度(Completeness)及最佳性(Optimal)來評論,A* 也是理想的,可完成度是高的,但最佳化還是要考慮heruistic。